Н

Зростаюча роль математики у розв'язанні задач науково-технічного прогресу країни становить перед школою задачу ефективної допомоги учням у оволодінні навчальним матеріалом і притаманним будь-якому предметові стилем мислення, який є важливим компонентом загальної культури сучасної людини. Підготовка учнів до самонавчання, виховання творчих інтересів нерозривно пов'язана зі зростанням інтелектуального потенціалу всього навчального процесу.

Проблема активізації пізнавальної діяльності учнів завжди була й залишається актуальною. Розв`язуючи її, педагогічні колективи прагнуть, щоб кожний урок допомагав у формуванні навчальних інтересів учнів, опануванні ними навичок самостійного поповнення знань. Високий рівень навчання геометрії залежить від удосконалення існуючих та пошуку нових прийомів і засобів активізації навчально-пізнавальної діяльності учнів. Тому тема, пов`язана з систематизацією, розробкою й удосконаленням методичних прийомів та засобів підвищення активності учнів при вивченні геометрії у 7 – 9 класах, є актуальною.

Мета роботи полягає в розробці методичної системи активізації навчально-пізнавальної діяльності учнів при засвоєнні курсу геометрії основної школи.

Об'єктом дослідження є навчальний процес з геометрії у 7 – 9 класах загальноосвітньої школи.

Предмет дослідження – використання прийомів і засобів активізації навчання геометрії в основній школі.

Психологічні основи проблеми пізнавальної активності учнів досліджували багато психологів, - зокрема, Л.С. Виготський, П.Я. Гальперін, О.М. Леонтьєв та ін.

Термін "активність" походить від латинського " activus", що означає діяльний, енергійний, ініціативний. Активність часто трактується як здатність змінювати навколишню дійсність у відповідності до особистих потреб, поглядів, мети. Як риса особливості, активність проявляє себе в енергійній, ініціативній діяльності. У свою чергу

свідоме навчання обов'язково передбачає активну діяльність учнів у цьому процесі. Пізнавальна активність – дійовий стан учня, який характеризується прагненням до навчання, проявом волі в процесі оволодіння знаннями. Активність учнів у навчанні характеризується їх ініціативністю та високим ступенем пізнавальної самостійності тощо.

Поняття "активізація навчально-пізнавальної діяльності учня" будемо трактувати як процес, спрямований на мобілізацію вчителем інтелектуальних, морально – вольових та фізичних сил учнів для досягнення конкретної мети навчання, розвитку та виховання, на посилену спільну навчально-пізнавальну діяльність учителя та учнів, на подолання інерції та пасивності у навчанні. Зауважимо, що активізацію навчання учнів не доцільно зводити до керівництва вчителем активністю учня, бо це водночас і процес активізації учнем своєї навчально-пізнавальної діяльності.

У роботах Я.Н. Грудьонова, М.Д. Кас`яненко, Р.С. Черкасова, А.А. Столяра доведено, що окремо взятий, ізольований від загальної системи навчання прийом (або метод) навчання не забезпечує продуктивної пізнавальної діяльності. Необхідно забезпечити реалізацію комплексного підходу до добору методів навчання, при якому ураховуються складові зв'язки і залежності між об`активними (мета, зміст) і суб`активними (учень з його індивідуальними можливостями та особливостями, колектив учнів класу в цілому) сторонами навчального процесу.

Внутрішніми стимулами навчально-пізнавальної діяльності виступають пізнавальні потреби, мотиви і інтереси учнів.

Доведено (М.Я. Ігнатенко, Ю.М. Колягін), що повноцінна активізація навчально-пізнавальної діяльності учнів передбачає дотримання ряду умов, зокрема - організацію навчально-пізнавальної діяльності учнів, що має починатися з чіткого формулювання вчителем мети, орієнтованої на конкретний кінцевий результат діяльності, і прийняття цієї мети учнями; систематичне формування потреби в оволодінні знаннями і уміннями, відповідних мотивів навчальної діяльності, інтересу до навчання; базовий зміст навчального матеріалу повинен бути доступним для учнів, а вимоги до його засвоєння – диференційованими за рівнями складності (обов`язковий, підвищений, поглиблений) тощо.

Рушійною силою процесу пізнання є внутрішні протиріччя між навчальними завданнями і вимогами до навчання та наявними можливостями учня. При навчанні математики безперервно поєднуються протилежні процеси: строго логічні міркування і уява, інтуїція; конкретне і абстрактне; індуктивні і дедуктивні міркування та ін. Найбільш поширеним протиріччям у навчально-пізнавальній діяльності є протиріччя між особистим досвідом учня і науковими знаннями з математики, які він набуває у школі. Саме ці протиріччя необхідно враховувати при розробці методичної системи активізації навчально-пізнавальної діяльності учнів.

Показниками навчально-пізнавальної активності є прагнення учнів до оперування набутими знаннями та уміннями, бажання поділитися з іншими (учнями, учителями, батьками) новою інформацією, потреба запитувати вчителя та ін.

Найчастіше виділяються такі рівні пізнавальної активності: нульовий; відносно – активний; виконавчо-активний; творчий.

У навчальному процесі використовують, як правило, три види контролю:

1) зовнішній контроль (його виконує вчитель над діяльністю учня);

2) взаємний контроль (виконують учні між собою за навчальною діяльністю один одного);

3) самоконтроль (його виконує учень самостійно над своєю навчальною діяльністю).

Зовнішній поточний і тематичний контроль мають велике значення для виявлення ефективності методичної системи роботи вчителя.

Взаємний контроль дозволяє учням порівнювати результати власної діяльності з заданими зразками або з результатами, які одержав товариш, виявити власні помилки і провести корекцію навчальної діяльності.

Самоконтроль сприяє міцному засвоєнню знань та виробленню способів навчальної діяльності. Самоконтроль - необхідна функція самоосвіти.

Ефективне формування математичних умінь учнів неможливо без активізації їх навчально-пізнавальної діяльності.

Основними напрямками активізації навчання математики при формуванні умінь учнів оперувати математичними поняттями та доводити математичні твердження є: чітке усвідомлення мети навчально-пізнавальної діяльності, орієнтованої на кінцевий результат; мотивація діяльності; забезпечення прикладної спрямованості діяльності.

При формуванні в учнів умінь розв`язувати задачі ефективними прийомами активізації є: диференціація задач за складністю; систематичне управління вчителем діяльністю учнів при розв`язуванні як стандартних, так і нестандартних задач; диференціація міри допомоги учням. Диференціація міри допомоги учням передбачає використання ланцюжків задач, допоміжних задач, зведення задачі до кількох під задач, складання карток – консультантів з навідними запитаннями, карток – інструкцій, картотеки опорних задач та ін.

Важливий напрям активізації навчально-пізнавальної діяльності становить застосування у навчальному процесі нових інформаційних технологій, які сприяють розширенню змістового наповнення курсу математики, інтенсифікації процесу навчання, його індивідуалізації та диференціації.

У своїх роботах Р.С.Черкасов, А.А.Столяр, Н.М. Рогановський підкреслюють, що впровадження нових інформаційних технологій навчання має бути педагогічно виправданим, тобто розглядатися за педагогічними перевагами перед традиційною методикою навчання і використовуватися в комплексі з іншими, зокрема традиційними засобами навчання.

Необхідною умовою підвищення ефективності шкільного навчання є розвиток пізнавальних сил учнів, що стимулюють їхню пізнавальну активність, спрямовану на оволодіння знаннями, безперервне їх поповнення і застосування. У цьому зв`язку стимулом такої діяльності є пізнавальний інтерес, що визначається як вибіркова націленість особистості, звернена до галузі пізнання. Закономірності точних наук викликають зацікавленість в учнів, що стимулює розвиток творчого мислення, впливає на індивідуальність. У результаті з`являється можливість для керування процесами пізнавальної діяльності учнів.

Проблема інтересу в навчанні не нова. Важливість його затверджували багато дидактів минулого. У самих різноманітних трактуваннях проблеми у класичній педагогіці головну функцію його бачили у тому, щоб приблизити учня до навчання, заохотити, "зачепити" так, щоб навчання для учня стало бажаним.

Увесь багатовіковий опит минулого дає основу стверджувати, що інтерес у навчанні являє собою важний фактор його побудови. Сучасна дидактика, спираючись на нові досягнення педагогіки і психології, бачить у інтересі ще більше можливостей і для навчання, і для розвитку, і для формування особистості учня у цілому.

Сьогодні проблема інтересу широко досліджується в контексті різноманітної діяльності учнів, що дозволяє творчим учителям, вихователям успішно формувати і розвивати інтереси учнів, збагачувати особистість, виховувати активне ставлення до життя.

Слід зауважити, що в учнів одного й того ж класу пізнавальний інтерес може мати різний рівень свого розвитку і різний характер прояви.

Елементарним рівнем пізнавального інтересу можна визнати відкритий, безпосередній інтерес до нових фактів, до цікавих явищ, які фігурують в інформації, одержаній учнем на уроці.

Більш високим рівнем його є інтерес до пізнання сущих властивостей предметів або явищ, які складають більш глибоку і часто невидиму їх внутрішню суть. Цей рівень вимагає пошуку, здогадки, активного оперування знаннями, які є в учня, здобутими способами.

На цьому рівні пізнавальний інтерес часто зв'язан з розв`язанням задач прикладного характеру, у яких учня цікавить не стільки принцип дії, скільки механізм, за допомогою якого вона відбувається. На цьому рівні інтерес вже не знаходиться на поверхні окремих фактів, але ще не проникає настільки в пізнання, щоб знайти закономірності.

Ще більш високий рівень пізнавального інтересу складає інтерес учня до причино – наслідних зв'язків, до виявлення закономірностей, до встановлення загальних принципів явищ, які діють у різних умовах. Цей рівень буває зв`язаний з елементами дослідницької творчої діяльності, з придбанням нових і удосконаленням попередніх способів навчання. На цьому рівні в учбовому процесі особливо відчувається посування учня, який виявляє не тільки схоплення загального смислу, але й глибоке усвідомлення важливих, суттєвих сторін досліджуваного матеріалу, який може бачити діалектику явищ, проявляти глибокий інтерес до пізнання закономірностей.

Вказаний головний параметр рівнів пізнавального інтересу – звертання до об'єктів пізнання (фактам, процесам, закономірностям) супроводжується ще й такими параметрами, як стійкість, локалізованість та усвідомленість, що слід мати на увазі при аналізі ролі пізнавального інтересу у структурі особи учня.

Параметри стійкості та локалізованості пізнавальних інтересів допомагають вчителю укріпити уявлення, які склалися, про рівні та характері інтересу до навчання своїх учнів і керуватися в учбовому процесі цим значимим мотивом навчання.

У комплексі даних про пізнавальний інтерес дуже суттєвим являється і його усвідомленість. Усвідомленість мотиву завжди пов'язана з більш сильнішим впливом його на діяльність. Неусвідомлений мотив також діє, але підспудно, тому їм трудніше управляти.

Незважаючи на те, що учні люблять активні форми діяльності – опити, практичні роботи, розв’язання проблемних питань і задач як на гуманітарних, так і на інших предметах, більш всього, однак, вони віддають перевагу інформації вчителя. Це означає, що до повідомлень учителів вони відносяться, як до самої повної, необхідної, логічно впорядкованої інформації, яка до того ж дає ключ до їх обґрунтованих відповідей, показує зразки систематизації учбового матеріалу і далеко виходить за рамки учбової книги. Таке відношення учнів високо піднімає престиж вчителя у сучасному учбовому процесі.

Надзвичайно важливо і те, що усвідомленість пізнавальних інтересів учнів дозволяє їм виказувати перевагу учбовим задачам більш складного характеру, до чого вони прагнуть при вільному виборі (наприклад, домашніх завдань, тем творів), у природній та експериментальній ситуаціях.

Відтак, пізнавальний інтерес треба признати одним з самих значимих факторів учбового процесу, вплив якого є не суперечним як на побудову світлої і радісної атмосфери навчання, так і на інтенсивність протікання пізнавальної діяльності учнів.

Ураховуючи величезний досвід минулого, спеціальні дослідження і практику сучасного досвіду, можна говорити про умови, дотримання яких сприяє формуванню, розвитку та зміцненню пізнавального інтересу учнів.

1. Максимальна опора на активну уявну діяльність учнів.

Підґрунтям для розвитку пізнавальних сил і можливостей учнів, як і для розвитку дійсно пізнавального інтересу, є ситуація розв`язування пізнавальних задач, ситуація активного напруження, протиріччя суджень, зіткнення різних позицій, в яких необхідно розібратися самому, прийняти рішення, визначити певну точку зору.

2. Друга умова, що забезпечує формування пізнавальних інтересів і особистості в цілому, полягає у проведенні навчального процесу на оптимальному рівні розвитку учнів.

Дослідження з метою перевірки ефективності дедуктивного шляху в пізнавальному процесі (Л.С. Виготський, О.І. Янцов) довели, що індуктивний шлях, що вважався класичним, не може повністю відповідати оптимальному розвитку учнів. Шлях узагальнення, відшукування закономірностей, яким підлягають очевидні явища і процеси, - це шлях, що у висвітленні багатьох питань і розділів науки сприяє більш високому рівню вивчення і засвоєння, оскільки спирається на максимальний рівень розвитку школяра. Саме ця умова забезпечує зміцнення і поглиблення пізнавального інтересу на підставі того, що навчання систематично й оптимально удосконалює діяльність пізнання, способів та вмінь.

У реальному процесі навчання учителю доводиться мати справу з постійним навчанням учнів багатьох умінь та навичок.

У навчанні математики важливими є уміння, які потребують розрахунків, точних обчислювань, використання калькулятора, циркуля, умінь, пов`язаних з просторовими уявленнями при зображенні рисунків, геометричних форм, фігур та ін.

З усього різноманіття предметних умінь виділяються загальні, якими учень може керуватися незалежно від змісту навчання, наприклад, такі, як уміння читати книгу (робота з книгою), аналізувати й узагальнювати, вміння систематизувати навчальний матеріал, виділяти одиничне, головне, логічно будувати відповідь, наводити докази тощо. Ці узагальнені вміння ґрунтуються на комплексі емоційних регулярних процесів. Вони складають ті способи пізнавальної діяльності, що дозволяють легко, мобільно, в різних умовах користуватися знаннями і за рахунок попередніх набувати нові.

Операційна сторона навчання не в меншій мірі, як змістова, пов'язана з мотиваційною. Саме з неї, з активних дій, з оперування знаннями поступають імпульси, які укріплюють пізнавальний інтерес. Спритність, здогадка, кмітливість, вмілість розкриваються у цьому оперуванні зі всією повнотою, і, чим повніше вони розкриваються, тим в більшій мірі отримує учень емоційне задоволення від своєї діяльності.

Пізнавальний інтерес учня не може розвиватися і міцніти, якщо операційна сторона навчання залишається постійною. В ній обов`язково потрібен поступових рух. Тільки тоді учень, оцінивши свої збільшені можливості і сили, усвідомлює, що тепер він по – іншому, по – новому, краще, легше, скоріше діє в учбовій обстановці. В цьому постійному ускладненні учбового труда, в оволодінні все більш складними і більш довершеними вміннями, які дозволяють розв`язувати складні задачі пізнання, і складається суть розвивального навчання, неухильно зміцнювального пізнавальних сил, інтересу і прагнення учня.

3. Емоційна атмосфера навчання, позитивний емоційний тонус навчального процесу – третя важлива умова.

Благополучна емоційна атмосфера навчання і учіння пов`язана з двома головними джерелами розвитку школяра: з діяльністю і спілкуванням, які створюють різноманітні стосунки і створюють тонус особистого настрою учня.

Обидва ці джерела не ізольовані один від одного, вони весь час переплітаються в навчальному процесі, і разом з тим стимули, що йдуть від них, різноманітні, як і різноманітні їх впливи на пізнавальну діяльність і інтерес до знань.

Кому не відомо, що благополучна емоційна ситуація діяльності забезпечує краще її протікання і результат! А між тим далеко не кожен учитель замислюється над всіма нюансами створювання цієї благополучної обстановки.

Наявність пізнавального інтересу визначено критеріями:

- виникнення питань, що вимагають дослідження причино – наслідкових зв`язків і розкриття закономірності;

- дослідницька активність, що спостерігається в ініціативності та самостійності;

- уміння учнів самостійно розв'язувати пізнавальні задачі, шукати вихід із проблемних ситуацій;

- підвищений інтерес до теоретичних знань, прагнення оволодіти цими знаннями, не зупинятись на тому, що вивчено на уроці. А самостійно поповнювати свої знання з різних джерел.

Зміст знань містить в собі і можливості по-новому проникнути в уже відоме, відкривати у тих знаннях, які є, нові грані, розглядати їх під новим кутом зору і відчути при цьому глибинні почуття задоволення від того, що тепер ти знаєш предмет краще, глибше і засновано.

Зміст знань не єдине джерело стимуляції пізнавального інтересу в учбовому процесі. Різноманітні стимули укріплення і формування інтересу до навчання поступають із самої діяльності учня, яка роджає інтелектуальні і емоційні задоволення.

Формування пізнавальної активності і самостійності учня в учбовому процесі – одне з таких направлень стимуляції. Це одна з означених ліній діяльності учителя, а сформованість активності і самостійності – важливий показник плодотворності навчання.

Проблема самостійної роботи учнів на уроці як головного стимулятора пізнавального інтересу, активності і розвитку особистості учня потребує від учителя дуже тонкої і глибокої роботи по відбору змісту самостійних робіт, їх форми, відповідності дидактичним призначенням і психологічним особливостям пізнавальних інтересів, а також означення їх місця в загальній структурі учбового процесу.

Розкриємо ще одне питання стимуляції пізнавального інтересу.

Мова іде про проблемність і елементи пошуку та дослідження в навчанні.

Процес розв`язування задач пошукового, дослідницького і творчого плану оперує більш складними психологічними структурами, зв`язаними з єдністю більш складних операційної і мотиваційної сторін діяльності. Наприклад, якщо учень має готовий алгоритм розв`язання стереотипної задачі, він робить у відповідності з жорстким приписом ряд послідовних операцій і не іспитує того інтелектуального напруження і емоційного піднесення, який відбувається у діяльності пошукової, дослідницької, при розв`язуванні проблемних ситуацій.

Озброювати школярів готовими способами розв`язання, нехай більш складними і значимими, також малоефективне, як і давати знання в готовому вигляді. Справжній успіх оволодіння новими способами для учіння і для розвитку навчає мого настане лише тоді, коли учень зазнає потребу, необхідність у новому способі, інакше кажучи, коли його мотиваційні стремління співпадуть з задачами навчання.

Але проводячи весь навчальний процес на рівні тільки проблемного навчання, учитель встає перед фактом зниження інтересу до знань. Треба чергувати проблемність з іншими методами. Це дає більше ефекту в укріпленні пізнавальних інтересів учнів.

Одним зі шляхів формування позитивного ставлення дітей до навчання є створення системи мотивів діяльності. Система мотивів піддається педагогічному управлінню і забезпечує визначення поведінки учнів та їх ставлення до вивчення того чи іншого навчального предмета.

Мотиваційна робота здійснюється переважно у двох напрямках: виховному і пізнавальному.

Тому групу методів стимулювання і мотивації навчання можна умовно поділити на дві великі підгрупи:

1) методи формування в школярів пізнавальних інтересів, що є прерогативою й обов'язком творчих груп учителів;

2) методи, спрямовані на формування почуття обов'язку і відповідальності в навчанні. Це є безпосереднім завданням учителів.

3) Процес формування позитивної мотивації до навчання, зокрема математики, полягає в здійсненні системи заходів. А саме:

- діагностика ставлення учнів до предмета (математики);

- вивчення особливостей психологічних процесів учнів;

- підбір форм, методів і прийомів викладання предмета відповідно до психологічних особливостей учнів;

- апробація вибраних форм, методів підвищення мотивації;

- активізація пізнавальних інтересів учнів до предмета.

- Тому можна запровадити такий шлях формування позитивної мотивації:

1.Проведення діагностики з використанням методики "Аналіз ставлення школярів до навчання".

2.Здійснення шкільним психологом діагностики особливостей розумових процесів: пам'яті, уваги, сприйняття, темпераменту кожного конкретного класу (учня) – та ознайомлення із отриманими даними вчителя-предметника.

3.Залежно від особливостей психологічних процесів, можна використовувати наведені нижче форми, методи та прийоми навчання.

Фронтальна. Учні виконують єдине для всіх завдання за єдиного для всіх темпу роботи. Вчитель працює одразу з усім класом, керує діяльністю усіх школярів, але врахувати індивідуальні особливості учнів не встигає, спираючись під час роботи на найбільш активних і підготовлених. Під час цієї форми роботи використовуються частково – пошуковий метод, робота з наочністю.

Індивідуальна. Характерна, на жаль, в основному для виконання домашніх завдань. Проте на уроці вона також має своє застосування. І вона ж дозволяє дотримуватися відмінностей у темпі навчання, враховуючи індивідуальні особливості учнів. За цієї форми роботи використовується як репродуктивний метод, так і дослідницький. Учні виконують завдання на порівняння об'єктів, складають їх характеристики за типовими планами, а також схеми, графіки, таблиці за матеріалами різних джерел знань.

Колективна. Діє схема "вчитель – колектив – учень": робота парами, бригадами і тимчасовими групами. Саме такі групи створюються під час навчальних рольових ігор та дискусій; застосовують групову форму на уроках узагальнюючого повторення, на семінарах, конференціях, диспутах, конкурсах.

У своїй практичній діяльності вчителі можуть використовувати набір різних видів методів – від репродуктивного до творчого мислення з послідовним ускладненням засобів діяльності, від пояснювально-демонстративного до дослідницького.

Особливу групу активних форм складають нестандартні типи уроків: уроки – лекції, уроки – мандрівки, уроки – конкурси, уроки – ділові ігри, бінарні та інтегровані уроки.

Математика та історія – дві нерозривні галузі знань. Відомості з історії математики, історичні задачі зближають ці шкільні предмети. Істрія збагачує математику гуманітарним та естетичним змістом, розвиває образне мислення учнів. Математика, розвиваючи логічне й системне мислення, в свою чергу посідає належне місце в історії, допомагає її краще зрозуміти. Як, розвиваючи проблему формування інтересу учнів до навчання, використовувати можливості цих шкільних предметів ? Відомості з історії математики, задачі історичного характеру, софізмі – це лише деякі "точки дотику" цих, здавалось б далеких, але достатньо близьких наук. Як домогтися того, щоб учні захопились математикою ? Як навчити їх розв'язувати задачі ? Як переконати в тому, що математика потрібна не лише в щоденному житті, а й у вивченні інших предметів?

Багато шкільних підручників математики розв'язують ці проблеми. Щоб розвивати інтерес учнів до предмета, вміщують цікаві задачі, системи вправ, що формують необхідні вміння і навички, прикладні питання, що показують зв`язок математики з іншими галузями знань. Звичайно, ми зустрічаємо в підручниках також історичні сторінки. Читаючи їх, дізнаємось про виникнення і розвиток математичних понять, виникнення і вдосконалення методів розв`язування задач.

І все ж таки творчому вчителю тісно в межах того історичного змісту, що подається в підручнику. Відомості з історії науки розширяють кругозір учнів, показують діалектику предмета. Тому так важливо, щоб історичні мотиви майстерно впліталися у тканину уроку математики, примушуючи дітей дивуватися, думати і захоплюватися незвичайною історією цієї багатогранної науки.

Форми викладання історичного матеріалу можуть бути різноманітні, починаючи від простих (бесіда вчителя, короткі повідомлення учнів на якусь тему, розв`язування історичних задач, розгадування софі змів, випуск стінгазет) до більш глибоких і складних, таких, як історико-математична конференція, захист рефератів з питань історії математики.

В програмах з математики, на жаль, на питання історичного характеру не відводиться жодної години, хоча відомо, що історія і математика нероздільні.

І все ж таки досвідчений учитель ніколи не починає викладання наступної теми, не сказавши про новий розділ математики, не починає без вступної історичної частини, що викликає інтерес та увагу учнів. Як, знайомлячи учнів з початковими поняттями геометрії, не розповісти про існування 13-ти книг Евкліда – "Начала". Знайомлячи учнів з побудовою правильних многокутників, знову згадуємо ім'я Евкліда. 13-ту книгу "Начал" присвячено Платоновим тілам – правильним многогранникам, красою яких захоплюємося на уроках стереометрії. Розглядаючи питання диференційного й інтегрального обчислення на уроках аналізу, говоримо про те, що ідеї, покладені в їх основу Ньютоном і Лейбніцом у 17 столітті, своїм корінням доходять до методу вичерпування, який відкрили свого часу Евклід та Архімед. Так історія математики допомагає зрозуміти не тільки логіку розвитку предмета, але й показує яскраві приклади вчених, які подолали нелегкий шлях відкриття істини.

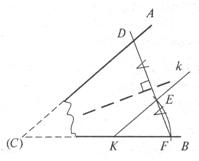
Відомо, що вже під час побудови першої єгипетської піраміди Джокера в Саккарі (близько 2800 р. до н. е.) давні зодчі були знайомі з правилами побудови так званих несумірних відрізків, тобто таких, довжини яких не можна виразити раціональним дробом. Разом з учнями можна виконати геометричну побудову і, повторюючи теорему Піфагора, ще раз обчислити довжини діагоналей прямокутників, зображених на рисунку. Так, знайомлячи на уроці з поняттям раціонального числа, можна геометрично та історично допомогти учням зрозуміти і відчути його суть (рис. 1).

Ефективним і зацікавлюючим прийомом є також математичний софізм. Софізм – це доведення свідомо хибного твердження. Причому помилка в доведенні майстерно замаскована. Групу давньогрецьких філософів, які жили в 5 – 4 ст. до н. е., називали софістами. Вони досягли великої майстерності в логіці.

Рис. 1

Учням 7 – 8 класів уже можна навести софізм про Ахіллеса й черепаху. Прудконогий Ахіллес, який бігає у 10 разів швидше за черепаху, не може її наздогнати. Нехай черепаха на 100 м попереду Ахіллеса. Коли Ахіллес пробігає ці 100 м, черепаха знаходиться від нього на 10 м. Пробігає Ахіллес і ці 10 м, а черепаха попереду на 1 м і т.д. Відстань між ними постійно скорочується, але ніколи не перетвориться в нуль. Отже, Ахіллес ніколи не наздожене черепаху.

Скільки захоплення, думок, сперечань, а головне – щирого інтересу й жадоби до знань викликає в учневі цей історичний софізм. Тут розглядаємо й чисто геометричне хибне твердження, намагаючись знайти майстерно замасковану помилку.

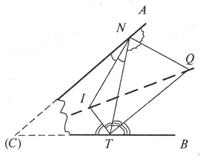
Доведемо, що всі ( ! ) трикутники рівнобедрені. Розглянемо довільний трикутник АВС. Проведемо в ньому бісектрису кута В і серединний перпендикуляр до сторони АС. Точку їх перетину позначимо через О. З точки О опустимо перпендикуляр ОЕ на сторону ВС. Неважко довести, що ОА = ОС і ОD = ОЕ. Отже, прямокутні трикутники АОD і СОЕ рівні за гіпотенузою і катетом. Звідси DАО = ЕСО. Крім того, ОАС = ОСА, оскільки трикутник АОС рівнобедрений (рис.2).

Рис. 2

Таким чином, дістаємо:

ВАС = DАО + ОАС = ЕСО + ОСА = ВСА.

Отже, ми довели, що ВАС = ВСА, а трикутник АВС – рівнобедрений і АВ = ВС.

Пошуки помилок привели до довгоочікуваного результату. Помилка виявилася у кресленні, адже серединний перпендикуляр до сторони і бісектриса протилежного їй кута для нерівнобедреного трикутника перетинаються поза цим трикутником.

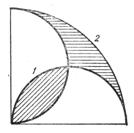
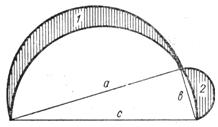
Учням була запропонована ще така задача. Гіпотенуза прямокутного трикутника лежить в площині р, один катет утворює з площиною р кут 45º, а другий – кут в 60º. Більший катет дорівнює а. Обчислити гіпотенузу (рис.3).

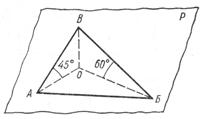
Рис. 3

Учень виконав креслення. З прямокутного трикутника АОВ знайшов ВО =

= а sin 45º = a , з прямокутного трикутника ОБВ знайшов БВ = ОВ:

sin 60º = а і по теоремі Піфагора АБ = а . Чи правильний отримано результат ?

Проведені міркування і викладки доводять лише таке: якщо прямокутний трикутник, про який ідеться в умові задачі, існує, то його гіпотенуза дорівнює а . Але саме існування такого трикутника нізвідки не виходить. Легко переконатися, що насправді такого трикутника не існує. У протилежному випадку величина плоского кута АБВ тригранного кута ВАОБ була б більшою суми величин двох інших плоских кутів АВД і ОВБ.

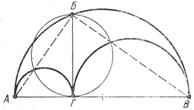
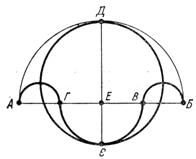
Красиві приклади рівно великості криволінійних фігур знайшов геніальний вчений Архімед. Найвідоміші з них – задачі обчислення площі кушнірського ножа або двогострої сокири (арбелона) і осьового перерізу сільниці (саліона), побудова яких очевидна (рис. 4).

Доведіть, що площа арбелона дорівнює площі круга з діаметром БГ, а площа саліона – площі круга з діаметром ДЄ.

Розв`язання: Sарб.= 1/2 (АВ/2)2 - 1/2(АГ/2)2 – – 1/2(ГВ/2)2 = /8 (АВ2 – АГ2 – ВГ2 ) = /8 ((АГ + + ГВ)2 – АГ2 – ГВ2) = /4 АГГВ = (ВГ/2)2.

Для обчислення Sсал. Легко встановлюється рівність: АБ2 + ГВ2 = 4(АЕ2 + ВЕ2) = 2 (ДЄ2 + АF2). Її можна подати у термінах відношення площ кругів: АБ2 + ГВ2 = 2(ДЄ2 + АF2), або 1/2АБ2 + + 1/2ГВ2 = ДЄ2 + АF2. Але АF2 = = 1/2 АF2 + 1/2АБ2, тому 1/2АБ2 + 1/2ГВ2 – – 1/2 АF2 - 1/2ВБ2 = ДЄ2. Що й потрібно було довести.

Ще приклад цікавої задачі: на радіусах чверті круга як на діаметрах побудовані півкруги. Яка з фігур має більшу площу – фігура 1 чи 2 ? (рис. 5)

Рис. 5.

Відповідь: площі рівні.

Задача: у квадрат зі стороною 1 кинули 51 точку. Доведіть, що принаймні три з них можна накрити кругом радіуса 1/7.

Розв'язання: розділимо квадрат прямими, паралельними сторонам, на 25 менших квадратиків із стороною 1/5. Якби в кожний квадратик потрапило не більше двох точок, то всього на 25 квадратиків потрапило б не більше 50 точок. Отже, знайдеться принаймні один квадратик, в який потрапили три точки. Оскільки діагональ цього квадратика менша, ніж 2/7 = , то цей квадратик можна покрити кругом діаметра 2/7.

Під час розв'язування геометричних задач на побудову в 7 – 8 класах звичайно ознайомимось з трьома давніми класичними задачами: про квадратуру круга, трисекцію кута й про подвоєння куба.

Вислів "квадратура круга" характеризує безвихідну, складну ситуацію. А почалося все в математиці і дуже давно. Коли цілком практичні задачі на обчислення площ привели до формулювання найзнаменитішої геометричної задачі давнини – квадратури круга: за допомогою лінійки без поділок і циркуля побудувати за скінченне число операцій квадрат, рівновеликий даному кругу. Надихаючим став приклад визначного математика античності Гіппократа Хінського ( 5 ст. до н.е.). Він зумів квадрувати три види фігур, обмежених дугами кіл (серпків Гіппократа). Наприклад, якщо на гіпотенузі с і катетах а і b прямокутного трикутника як по діаметрах побудувати півкруги, то сума площ заштрихованих серпків Гіппократа рівновелика площі даного трикутника (рис.6).

Рис.6

Позначивши довжину гіпотенузи і катетів трикутника відносно через с, а, b, доведіть, що S1 + S2 = ½ ab.

Розв'язання: Sсерпк. = 1/8 + 1/8а2 - 1/8с2 + 1/2аb =1/8( а2 + b2 – с2) +

+ 1/2аb = 1/80 + 1/2аb = 1/2аb.

Із задоволенням та емоційним піднесенням слухають учні легенду, що пов`язана з "делоською задачею" про подвоєння куба. Свою назву вона дістала від острова Делос в Егейському морі, на якому, за легендою, щоб врятувати мешканців від епідемії, оракул наказав подвоїти олтар, що мав форму куба.

Учні дізнаються про те, що давні задачі не можна розв`язати за допомогою циркуля і лінійки, але завдяки багаторічним пошукам їх розв'язання удосконалились математичні методи. Історично розвивалась і сама математика.

Добре відома задача Евкліда: побудуйте бісектрису кута, вершина якого недоступна. Навряд чи знайдеться учень, який не захоче розв'язати її. Хіба не дивно: самого кута немає, а його бісектрису провести можна! Задача Евкліда настільки емоційна, що, справді, неможливо утриматися від бажання скласти нові задачі, імпровізувати на цю тему. Що аматори геометрії з успіхом і роблять. У результаті через 2300 років склалася "симпатична" колекція задач, яку можна сміливо назвати гімном Евкліду!

Що стосується самої задачі Евкліда, то існує 7 – 8 способів її розв`язування. Два з них ми пропонуємо увазі учнів.

Отже, побудуйте бісектрису кута, вершина якого недоступна.

Розв'язання: 1 спосіб. Нехай вершина С кута АВС недоступна (рис. 7).

Рис. 7

Проведемо через довільну точку К, яка належить ВС, пряму к паралельну АС. З точки К як з центра проведемо довільне коло й дістанемо в результаті перетину з к і ВС точки Е й F відповідно. При цьому КЕ = КF. Продовжимо FE до перетину з АС у точці D. Очевидно, що трикутник DCF (з недоступною вершиною С) є рівнобедреним. Тоді серединний перпендикуляр до DF збіжиться з бісектрисою кута С.

2 спосіб. Проведемо довільно відрізок NT (N AC, T ВС) – рис. 8. Нехай внутрішні бісектриси кутів N і T трикутника NСT перетнуться в точці І.

Рис. 8

Зовнішні ж бісектриси кутів N і T нехай перетинаються в точці Q. Пряма QI збіжиться з бісектрисою кута С (доведіть!).

Методичні рекомендації по активізації навчально-пізнавальної діяльності учнів, по формуванню пізнавального інтересу ми представляємо у вигляді конспектів уроків по різноманітним темам курсу планіметрії. Запропоновані нами завдання, які супроводжуються викладанням цікавих способів їх розв`язування, виключають шаблонний підхід, завчання готових схем. Вони розраховані на пробудження творчої активності учнів і носять пошуковий характер.

Отак, по волі учнів просторові фігури не тільки "оселилися" на уроках геометрії у 7 – 9 класах, але й прийшли до руху. Опит показує, що нескладні задачі з "виходом у простір" дають більше можливості для творчості учнів. Такі задачі розв`язуються більш вільно, так як усі розуміють, що матеріал дається "на зріст", він не обов`язковий для бистрого засвоєння. Може бути, ця необов`язковість і приковує увагу учнів, бо для кожного з них важливо справитися зі складною задачею.

Може постати питання – навіщо знову й знову доводити відому теорему? Чи це не є такою собі своєрідною інтелектуальною розвагою? Різні доведення тієї чи іншої теореми дають змогу краще осмислити її місце в системі математичних знань, спонукають до аналізу засобів, що використовуються в міркуваннях. А таке осмислення і такий аналіз відіграють важливу роль у формуванні сучасного математичного стилю мислення, який яскраво виявляє себе у системному методі наукових досліджень, в інформатиці, у побудові навчальних курсів.

Доцільно звернути увагу також на мотиви математичного пошуку. Звичайно, з точки зору обчислювальної практики площу чотирикутника можна знайти як суму площ двох трикутників, об'єм трикутної піраміди легко знаходимо за висотою і площею основи. Тому узагальнення формули Герона важливі швидше з естетичної точку зору – але "двовимірне" узагальнення за схемою "трикутник – чотирикутник" (по горизонталі) і "трикутник – тетраедр" (по вертикалі) надає довершеності нашим знанням про формулу Герона.

Однак з теоретичної точки зору ці узагальнення не продуктивні. В сучасній математиці важливу роль відіграють η-вимірні простори, окремими випадками яких є площина і тривимірний простір. Намагання ж одержати η-вимірний аналог формули Герона навряд чи були б виправдані. І це теж повчальний урок – не кожна ідея здатна постійно розвиватися.

Висновки.

При виконанні аналізу та розробці методики активізації навчально-пізнавальної діяльності учнів, необхідно виділяти зв`язки між об`єктивними ( мета, зміст навчального предмету ) та суб`єктивними ( учень з його індивідуальними можливостями та особливостями, колектив учнів класу в цілому ) сторонами навчального процесу.

До основних умов активізації навчально-пізнавального процесу доцільно віднести:

- виділення вчителем мети вивчення окремих тем, орієнтованої на кінцевий результат, та прийняття її учнями (мотивація вивчення той чи іншої теми);

- систематичне формування в учнів потреби в оволодінні знаннями та уміннями, відповідних мотивів навчальної діяльності, пізнавального інтересу до навчання;

- базовий зміст навчального матеріалу повинен бути доступним для учнів, а вимоги до його засвоєння – диференційованими за рівнем складності;

- використання, а потім і самостійне конструювання учнями орієнтовних основ дій для розв'язання навчальних задач;

- використання методів проблемного навчання;

- ретельне структурування змісту навчального матеріалу та програмування діяльності учнів.

Серед названих умов пізнавальний інтерес – один з основних факторів розвитку активності і самостійності навчання учня. Рівні розвитку пізнавального інтересу, його цінність в учбовому процесі, вміння розпізнавати інтерес до навчання у школярів, умови формування інтересу до знань – все це впливає на активізацію навчально-пізнавальної діяльності учнів.

Формуванню пізнавального інтересу сприяють зміст учбового матеріалу , самостійна діяльність учнів, змінення відношення у методиці навчання між інформативними і активними методами, проблемність та елементи пошуку і дослідження у навчанні.

Розглядання однієї з важливіших проблем сучасної дидактики – формування пізнавальних інтересів учнів слід закінчити декількома узагальненнями.

1. Розглядання пізнавального інтересу як елементу розвивального навчання, підкреслює, що він один з самих значимих мотивів учіння, формуючи який ми створюємо прочну і надійну основу особистості школяра.

2. За допомогою пізнавального інтересу показуємо складність та значимість внутрішньої сторони навчання, яка постійно повинна бути у полі зору вчителя. Кожна задача, яка пропонована учневі, кожна його учбова дія визиває багато психічних процесів, від характеру протікання яких часто залежить навчання та учіння. При наявності пізнавальних інтересів учіння становиться близькою, життєво значимою діяльністю, у якій сам школяр дуже зацікавлений.

3. У навчальному процесі в першу чергу лежать джерела справжнього пізнавального інтересу. Цей процес, який володіє означеним змістом учбових предметів, організує операційну діяльність учнів, володіє і значними об`єктивними можливостями стимуляції пізнавальних інтересів. В свою чергу пізнавальний інтерес учнів у навчанні являється джерелом енергетичних ресурсів діяльності учнів.